This module implements "factor model" for representing an incomplete matrix using a low-rank approximation [1]. Mathematically, this model seeks to find matrices U and V (also referred as factors) that, for any given incomplete matrix A, minimizes:
![\[ \|\boldsymbol A - \boldsymbol UV^{T} \|_2 \]](form_47.png)
subject to 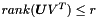 , where
, where 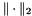 denotes the Frobenius norm. Let
denotes the Frobenius norm. Let 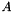 be a
be a 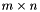 matrix, then
matrix, then 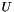 will be
will be 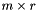 and
and 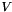 will be
will be 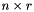 , in dimension, and
, in dimension, and 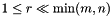 . This model is not intended to do the full decomposition, or to be used as part of inverse procedure. This model has been widely used in recommendation systems (e.g., Netflix [2]) and feature selection (e.g., image processing [3]).
. This model is not intended to do the full decomposition, or to be used as part of inverse procedure. This model has been widely used in recommendation systems (e.g., Netflix [2]) and feature selection (e.g., image processing [3]).
Low-rank matrix factorization of an incomplete matrix into two factors.
lmf_igd_run( rel_output,
rel_source,
col_row,
col_column,
col_value,
row_dim,
column_dim,
max_rank,
stepsize,
scale_factor,
num_iterations,
tolerance
)
Arguments
TEXT. The name of the table to receive the output.
Output factors matrix U and V are in a flattened format.
RESULT AS (
matrix_u DOUBLE PRECISION[],
matrix_v DOUBLE PRECISION[],
rmse DOUBLE PRECISION
);Features correspond to row i is matrix_u[i:i][1:r]. Features correspond to column j is matrix_v[j:j][1:r].
TEXT. The name of the table containing the input data.
The input matrix> is expected to be of the following form:
{TABLE|VIEW} input_table (
row INTEGER,
col INTEGER,
value DOUBLE PRECISION
)Input is contained in a table that describes an incomplete matrix, with available entries specified as (row, column, value). The input matrix should be 1-based, which means row >= 1, and col >= 1. NULL values are not expected.
DROP TABLE IF EXISTS lmf_data; CREATE TABLE lmf_data ( row INT, col INT, val FLOAT8 );
INSERT INTO lmf_data VALUES (1, 1, 5.0); INSERT INTO lmf_data VALUES (3, 100, 1.0); INSERT INTO lmf_data VALUES (999, 10000, 2.0);
DROP TABLE IF EXISTS lmf_model;
SELECT madlib.lmf_igd_run( 'lmf_model',
'lmf_data',
'row',
'col',
'val',
999,
10000,
3,
0.1,
2,
10,
1e-9
);
Example result (the exact result may not be the same).
NOTICE:
Finished low-rank matrix factorization using incremental gradient
DETAIL:
table : lmf_data (row, col, val)
Results:
RMSE = 0.0145966345300041
Output:
view : SELECT * FROM lmf_model WHERE id = 1
lmf_igd_run
-----------
1
(1 row)
SELECT array_dims(matrix_u) AS u_dims, array_dims(matrix_v) AS v_dims FROM lmf_model WHERE id = 1;Result:
u_dims | v_dims
--------------+----------------
[1:999][1:3] | [1:10000][1:3]
(1 row)
SELECT matrix_u[2:2][1:3] AS row_2_features FROM lmf_model WHERE id = 1;Example output (the exact result may not be the same):
row_2_features
---------------------------------------------------------
{{1.12030523084104,0.522217971272767,0.0264869043603539}}
(1 row)
SELECT madlib.array_dot(
matrix_u[2:2][1:3],
matrix_v[7654:7654][1:3]
) AS row_2_col_7654
FROM lmf_model
WHERE id = 1;
Example output (the exact result may not be the same due the randomness of the algorithm): row_2_col_7654 ------------------ 1.3201582940851 (1 row)
[1] N. Srebro and T. Jaakkola. “Weighted Low-Rank Approximations.” In: ICML. Ed. by T. Fawcett and N. Mishra. AAAI Press, 2003, pp. 720–727. isbn: 1-57735-189-4.
[2] Simon Funk, Netflix Update: Try This at Home, December 11 2006, http://sifter.org/~simon/journal/20061211.html
[3] J. Wright, A. Ganesh, S. Rao, Y. Peng, and Y. Ma. “Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices via Convex Optimization.” In: NIPS. Ed. by Y. Bengio, D. Schuurmans, J. D. Lafferty, C. K. I. Williams, and A. Culotta. Curran Associates, Inc., 2009, pp. 2080–2088. isbn: 9781615679119.