Principal component projection is a mathematical procedure that projects high dimensional data onto a lower dimensional space. This lower dimensional space is defined by the 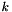 principal components with the highest variance in the training data.
principal components with the highest variance in the training data.
More details on the mathematics of PCA can be found in Principal Component Analysis and some details about principal component projection calculations can be found in the Technical Background.
madlib.pca_project( source_table,
pc_table,
out_table,
row_id,
residual_table,
result_summary_table
)
For sparse matrices:
madlib.pca_sparse_project( source_table,
pc_table,
out_table,
row_id,
col_id, -- Sparse matrices only
val_id, -- Sparse matrices only
row_dim, -- Sparse matrices only
col_dim, -- Sparse matrices only
residual_table,
result_summary_table
)
Arguments
TEXT. Source table name. Identical to pca_train, the input data matrix should have 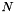 rows and
rows and 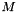 columns, where
columns, where 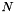 is the number of data points, and
is the number of data points, and 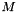 is the number of features for each data point.
is the number of features for each data point.
The input table for pca_project is expected to be in the one of the two standard MADlib dense matrix formats, and the sparse input table for pca_sparse_project should be in the standard MADlib sparse matrix format. These formats are described in the documentation for Principal Component Analysis.
TEXT. Table name for the table containing principal components.
TEXT. Name of the table that will contain the low-dimensional representation of the input data.
The out_table encodes a dense matrix with the projection onto the principal components. The table has the following columns:
| row_id | Row id of the output matrix. |
|---|---|
| row_vec | A vector containing elements in the row of the matrix. |
TEXT. Column name containing the row IDs in the input source table. The column should be of type INT (or a type that can be cast to INT) and should only contain values between 1 and N. For dense matrix format, it should contain all continguous integers from 1 to N describing the full matrix.
TEXT. Column name containing the column IDs in sparse matrix representation. The column should be of type INT (or a type that can be cast to INT) and should only contain values between 1 and M. This parameter applies to sparse matrices only.
TEXT. Name of 'val_id' column in sparse matrix representation defining the values of the nonzero entries. This parameter applies to sparse matrices only.
INTEGER. The actual number of rows in the matrix. That is, if the matrix was transformed into dense format, this is the number of rows it would have. This parameter applies to sparse matrices only.
INTEGER. The actual number of columns in the matrix. That is, if the matrix was transformed into dense format, this is the number of columns it would have. This parameter applies to sparse matrices only.
TEXT, default: NULL. Name of the optional residual table.
The residual_table encodes a dense residual matrix. The table has the following columns:
| row_id | Row id of the output matrix. |
|---|---|
| row_vec | A vector containing elements in the row of the residual matrix. |
TEXT, default: NULL. Name of the optional summary table.
The result_summary_table contains information about the performance time of the PCA projection. The table has the following columns:
| exec_time | Elapsed time (ms) for execution of the function. |
|---|---|
| residual_norm | Absolute error of the residuals. |
| relative_residual_norm | Relative error of the residuals. |
SELECT madlib.pca_project();
DROP TABLE IF EXISTS mat;
CREATE TABLE mat (id integer,
row_vec double precision[]
);
INSERT INTO mat VALUES
(1, '{1,2,3}'),
(2, '{2,1,2}'),
(3, '{3,2,1}');
DROP TABLE IF EXISTS result_table, result_table_mean;
SELECT madlib.pca_train('mat', -- Source table
'result_table', -- Output table
'id', -- Row id of source table
2); -- Number of principal components
SELECT * FROM result_table ORDER BY row_id;
row_id | principal_components | std_dev | proportion
--------+--------------------------------------------------------------+-------------------+-------------------
1 | {0.707106781186547,-6.93889390390723e-18,-0.707106781186548} | 1.41421356237309 | 0.857142857142244
2 | {0,1,0} | 0.577350269189626 | 0.142857142857041
(2 rows)
DROP TABLE IF EXISTS residual_table, result_summary_table, out_table;
SELECT madlib.pca_project( 'mat',
'result_table',
'out_table',
'id',
'residual_table',
'result_summary_table'
);
SELECT * FROM out_table ORDER BY row_id;
row_id | row_vec
--------+--------------------------------------
1 | {-1.41421356237309,-0.33333333333}
2 | {2.77555756157677e-17,0.66666666667}
3 | {1.41421356237309,-0.33333333333}
(3 rows)
Check the error in the projection: SELECT * FROM result_summary_table;
exec_time | residual_norm | relative_residual_norm ---------------+-------------------+------------------------ 331.792116165 | 5.89383520611e-16 | 9.68940539229e-17 (1 row)Check the residuals:
SELECT * FROM residual_table ORDER BY row_id;
row_id | row_vec
--------+--------------------------------------------------------------------
1 | {-2.22044604925031e-16,-1.11022302462516e-16,3.33066907387547e-16}
2 | {-1.12243865646685e-18,0,4.7381731349413e-17}
3 | {2.22044604925031e-16,1.11022302462516e-16,-3.33066907387547e-16}
(3 rows)
DROP TABLE IF EXISTS mat_group;
CREATE TABLE mat_group (
id integer,
row_vec double precision[],
matrix_id integer
);
INSERT INTO mat_group VALUES
(1, '{1,2,3}', 1),
(2, '{2,1,2}', 1),
(3, '{3,2,1}', 1),
(4, '{1,2,3,4,5}', 2),
(5, '{2,5,2,4,1}', 2),
(6, '{5,4,3,2,1}', 2);
DROP TABLE IF EXISTS result_table_group, result_table_group_mean;
SELECT madlib.pca_train('mat_group', -- Source table
'result_table_group', -- Output table
'id', -- Row id of source table
0.8, -- Proportion of variance
'matrix_id'); -- Grouping column
SELECT * FROM result_table_group ORDER BY matrix_id, row_id;
row_id | principal_components | std_dev | proportion | matrix_id
--------+------------------------------------------------------------------------------------------------+-----------------+-------------------+-----------
1 | {0.707106781186548,0,-0.707106781186547} | 1.4142135623731 | 0.857142857142245 | 1
1 | {-0.555378486712784,-0.388303582074091,0.0442457354870796,0.255566375612852,0.688115693174023} | 3.2315220311722 | 0.764102534485173 | 2
2 | {0.587384101786277,-0.485138064894743,0.311532046315153,-0.449458074050715,0.347212037159181} | 1.795531127192 | 0.235897465516047 | 2
(3 rows)
DROP TABLE IF EXISTS mat_group_projected;
SELECT madlib.pca_project('mat_group',
'result_table_group',
'mat_group_projected',
'id');
SELECT * FROM mat_group_projected ORDER BY matrix_id, row_id;
row_id | row_vec | matrix_id
--------+---------------------------------------+-----------
1 | {1.4142135623731} | 1
2 | {7.40148683087139e-17} | 1
3 | {-1.4142135623731} | 1
4 | {-3.59290479201926,0.559694003674779} | 2
5 | {0.924092949098971,-2.00871628417505} | 2
6 | {2.66881184290186,1.44902228049511} | 2
(6 rows)
DROP TABLE IF EXISTS mat_sparse;
CREATE TABLE mat_sparse (
row_id integer,
col_id integer,
value double precision
);
INSERT INTO mat_sparse VALUES
(1, 1, 1.0),
(2, 2, 2.0),
(3, 3, 3.0),
(4, 4, 4.0),
(1, 5, 5.0),
(2, 4, 6.0),
(3, 2, 7.0),
(4, 3, 8.0);
As an aside, this is what the sparse matrix above looks like when put in dense form:
DROP TABLE IF EXISTS mat_dense;
SELECT madlib.matrix_densify('mat_sparse',
'row=row_id, col=col_id, val=value',
'mat_dense');
SELECT * FROM mat_dense ORDER BY row_id;
row_id | value
--------+-------------
1 | {1,0,0,0,5}
2 | {0,2,0,6,0}
3 | {0,7,3,0,0}
4 | {0,0,8,4,0}
(4 rows)
DROP TABLE IF EXISTS result_table, result_table_mean;
SELECT madlib.pca_sparse_train( 'mat_sparse', -- Source table
'result_table', -- Output table
'row_id', -- Row id of source table
'col_id', -- Column id of source table
'value', -- Value of matrix at row_id, col_id
4, -- Actual number of rows in the matrix
5, -- Actual number of columns in the matrix
3); -- Number of principal components
SELECT * FROM result_table ORDER BY row_id;
Result (with principal components truncated for readability):
row_id | principal_components | std_dev | proportion
--------+----------------------------------------------+------------------+-------------------
1 | {-0.0876046030186158,-0.0968983772909994,... | 4.21362803829554 | 0.436590030617467
2 | {-0.0647272661608605,0.877639526308692,... | 3.68408023747461 | 0.333748701544697
3 | {-0.0780380267884855,0.177956517174911,... | 3.05606908060098 | 0.229661267837836
(3 rows)
DROP TABLE IF EXISTS mat_sparse_out;
SELECT madlib.pca_sparse_project(
'mat_sparse',
'result_table',
'mat_sparse_out',
'row_id',
'col_id',
'value',
4,
5
);
SELECT * FROM mat_sparse_out ORDER BY row_id;
row_id | row_vec
--------+---------------------------------------------------------
1 | {4.66617015032369,-2.63552220635847,2.1865220849604}
2 | {0.228360685652383,-1.21616275892926,-4.46864627611561}
3 | {0.672067460100428,5.45249627172823,0.56445525585642}
4 | {-5.5665982960765,-1.6008113064405,1.71766893529879}
(4 rows)
DROP TABLE IF EXISTS mat_sparse_group;
CREATE TABLE mat_sparse_group (
row_id integer,
col_id integer,
value double precision,
matrix_id integer);
INSERT INTO mat_sparse_group VALUES
(1, 1, 1.0, 1),
(2, 2, 2.0, 1),
(3, 3, 3.0, 1),
(4, 4, 4.0, 1),
(1, 5, 5.0, 1),
(2, 4, 6.0, 2),
(3, 2, 7.0, 2),
(4, 3, 8.0, 2);
DROP TABLE IF EXISTS result_table_group, result_table_group_mean;
SELECT madlib.pca_sparse_train( 'mat_sparse_group', -- Source table
'result_table_group', -- Output table
'row_id', -- Row id of source table
'col_id', -- Column id of source table
'value', -- Value of matrix at row_id, col_id
4, -- Actual number of rows in the matrix
5, -- Actual number of columns in the matrix
0.8, -- Proportion of variance
'matrix_id');
SELECT * FROM result_table_group ORDER BY matrix_id, row_id;
Result (with principal components truncated for readability):
row_id | principal_components | std_dev | proportion | matrix_id
--------+--------------------------------------------+------------------+-------------------+-----------
1 | {-0.17805696611353,0.0681313257646983,... | 2.73659933165925 | 0.544652792875481 | 1
2 | {-0.0492086814863993,0.149371585357526,... | 2.06058314533194 | 0.308800210823714 | 1
1 | {0,-0.479486114660443,... | 4.40325305087975 | 0.520500333693473 | 2
2 | {0,0.689230898585949,... | 3.7435566458567 | 0.376220573442628 | 2
(4 rows)
DROP TABLE IF EXISTS mat_sparse_group_projected;
SELECT madlib.pca_sparse_project(
'mat_sparse_group',
'result_table_group',
'mat_sparse_group_projected',
'row_id',
'col_id',
'value',
4,
5
);
SELECT * FROM mat_sparse_group_projected ORDER BY matrix_id, row_id;
row_id | row_vec | matrix_id
--------+-----------------------------------------+-----------
1 | {-4.00039298524261,-0.626820612715982} | 1
2 | {0.765350785238575,0.951348276645455} | 1
3 | {1.04951017256904,2.22388180170356} | 1
4 | {2.185532027435,-2.54840946563303} | 1
1 | {-0.627846810195469,-0.685031603549092} | 2
2 | {-1.64754249747757,-4.7662114622896} | 2
3 | {-3.98424961281857,4.13958468655255} | 2
4 | {6.25963892049161,1.31165837928614} | 2
(8 rows)
Given a table containing some principal components 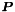 and some input data
and some input data 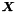 , the low-dimensional representation
, the low-dimensional representation 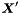 is computed as
is computed as
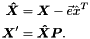
where 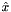 is the column means of
is the column means of 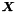 and
and 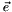 is the vector of all ones. This step is equivalent to centering the data around the origin.
is the vector of all ones. This step is equivalent to centering the data around the origin.
The residual table 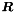 is a measure of how well the low-dimensional representation approximates the true input data, and is computed as
is a measure of how well the low-dimensional representation approximates the true input data, and is computed as
![\[ {\boldsymbol R} = {\boldsymbol {\hat{X}}} - {\boldsymbol X}' {\boldsymbol P}^T. \]](form_236.png)
A residual matrix with entries mostly close to zero indicates a good representation.
The residual norm 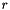 is simply
is simply
![\[ r = \|{\boldsymbol R}\|_F \]](form_238.png)
where 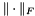 is the Frobenius norm. The relative residual norm
is the Frobenius norm. The relative residual norm 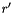 is
is
![\[ r' = \frac{ \|{\boldsymbol R}\|_F }{\|{\boldsymbol X}\|_F } \]](form_241.png)